The goal of teaching-learning, from a dialogical perspective, is that the student appropriate mathematical discourse, which means not only assimilating it, but also adapting it creatively to his or her own “semantic and expressive intention” (Bakhtin, 1986, pp. 293 - 294). Bakhtin distinguishes two competing characteristics of discourse: authoritative discourse and internally persuasive discourse. Authoritative discourse is a discourse that only expresses a single perspective and demands acceptance. It is discourse of officially accepted knowledge, such as is found in textbooks, government policy documents, and from the mouths of teachers. It is a characteristic often associated with traditional teaching, where students are expected to assent to, and internalise, the presented content, without having their own perspectives having impact on the content. Internally persuasive discourse is discourse that resonates with us, that enters into an interaction, and struggle, with our other internally persuasive discourses, all our other “available verbal and ideological points of view, approaches, directions and values” (Bakhtin, 1981, p. 346). Internally persuasive discourse is not simply taken as given, but developed further, “applied to new material, new conditions; it enters into interanimating relationships with new contexts” (Bakthin, 1981, p. 346). It is the discourse of our personal beliefs, the ideas that move us, that shape us and create the stories we tell ourselves about the world and who we are (Landay, 2004).

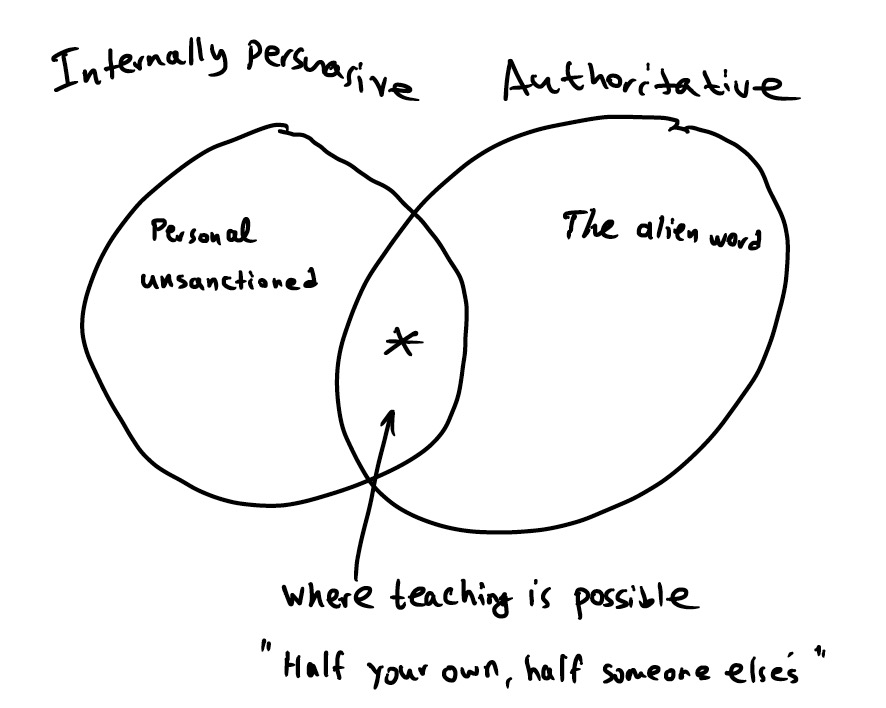
Discourse can simultaneously have authoritative and internally persuasive qualities. Teaching-learning happens precisely when both of these qualities go together, at their points of intersection. When authoritative discourse becomes an internally persuasive discourse, in interaction with our prior internally persuasive discourses, it expands our action- and meaning making potential. Learning mathematics, then, includes expanding our internally persuasive discourse to include as a creative resource the historically established ways of communicating of academic mathematical discourse.

Dialogic teaching

• In a dialogic classroom, the students’ perspectives and discourses are valued, but there remains the problem of connecting these with mathematical discourse.
• It’s not enough that students speak. Their internally persuasive discourse must be challenged, it must enter into a struggle. It must touch the authoritative.

References:

Bakhtin, M. M. (1981). The dialogic imagination: Four essays. University of Texas Press.

Bakhtin, M. M. (1986). Speech Genres and Other Late Essays. University of Texas Press.

Landay, E. (2004). Performance as the foundation for a secondary school literacy program: A Bakhtinian perspective. In A. F. Ball & S. Warshauer Freedman (Eds.), Bakhtinian perspectives on language, literacy, and learning (pp. 107–128). Cambridge University Press.